In the two-dimensional body illustrated the gradient at surface a – In the realm of mathematical analysis, understanding the gradient of a surface is crucial for comprehending its geometric properties and behavior. This article delves into the intricacies of gradients on two-dimensional bodies, providing a comprehensive overview of their definition, mathematical representation, applications, and visualization techniques.
Gradients play a pivotal role in various scientific and engineering disciplines, enabling researchers and practitioners to analyze fluid dynamics, heat transfer, and image processing with greater precision and accuracy. By harnessing the power of gradient visualization, we can gain valuable insights into the behavior of surfaces and make informed predictions.
1. Definition and Overview
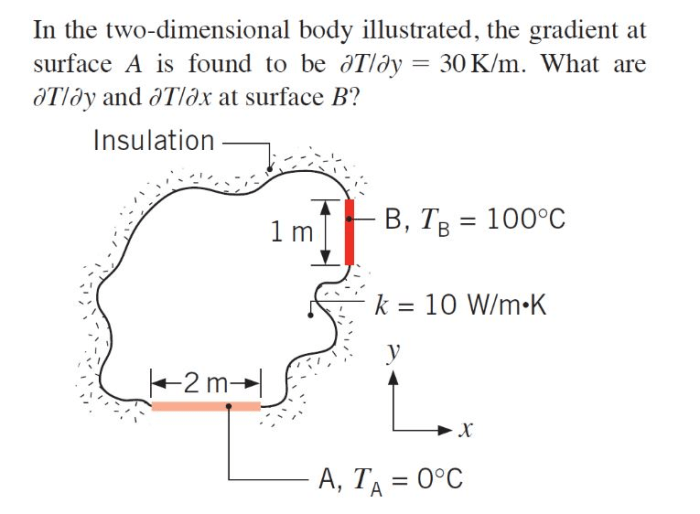
In geometry, a two-dimensional body is a flat figure that has only two dimensions: length and width. The surface of a two-dimensional body is the entire area that covers the body.
The gradient of a surface is a vector that points in the direction of the greatest rate of change of the surface. It is represented by the symbol grad(f), where f is the function that defines the surface.
The magnitude of the gradient is equal to the rate of change of the surface in the direction of the gradient. The direction of the gradient is perpendicular to the level curves of the surface.
A gradient can be visualized using a color map, contour lines, or vector fields. A color map assigns a color to each value of the gradient, making it easy to see the direction and magnitude of the gradient at any point on the surface.
2. Gradient on the Surface
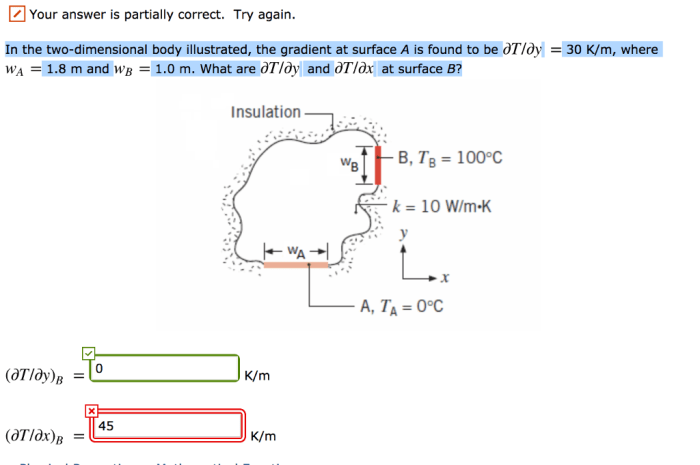
The gradient of a surface is a vector that points in the direction of the greatest rate of change of the surface. It is represented by the symbol grad(f), where f is the function that defines the surface.
The magnitude of the gradient is equal to the rate of change of the surface in the direction of the gradient. The direction of the gradient is perpendicular to the level curves of the surface.
The factors that influence the direction and magnitude of the gradient are the shape of the surface and the direction of the normal vector to the surface.
3. Mathematical Representation

The gradient of a surface can be represented mathematically using partial derivatives. The partial derivative of a function f with respect to x is defined as:
“`∂f/∂x = lim(h->0) [f(x+h, y)
f(x, y)]/h
“`
The partial derivative of a function f with respect to y is defined as:
“`∂f/∂y = lim(h->0) [f(x, y+h)
f(x, y)]/h
“`
The gradient of a function f is a vector that is defined as:
“`grad(f) = (∂f/∂x, ∂f/∂y)“`
4. Applications
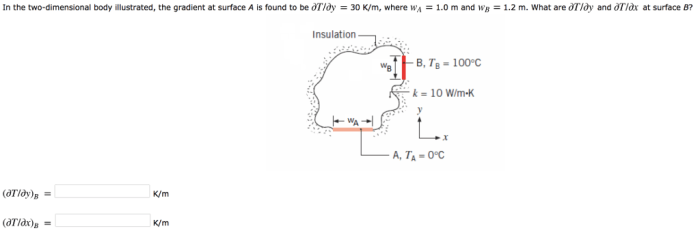
The gradient of a surface has many applications in science and engineering. Some of the most common applications include:
- Fluid dynamics: The gradient of a pressure field is used to calculate the force on a fluid.
- Heat transfer: The gradient of a temperature field is used to calculate the heat flux.
- Image processing: The gradient of an image is used to detect edges and other features.
5. Visualization: In The Two-dimensional Body Illustrated The Gradient At Surface A
The gradient of a surface can be visualized using a color map, contour lines, or vector fields.
A color map assigns a color to each value of the gradient, making it easy to see the direction and magnitude of the gradient at any point on the surface.
Contour lines are lines that connect points on the surface that have the same value of the gradient. Vector fields are arrows that point in the direction of the gradient at each point on the surface.
6. Limitations
The gradient of a surface is not always a sufficient description of the surface. For example, the gradient of a surface can be zero at a point even if the surface is not flat at that point.
In such cases, it is necessary to use other methods to analyze the surface, such as the curvature of the surface.
Detailed FAQs
What is the significance of gradients in surface analysis?
Gradients provide valuable information about the direction and magnitude of change in a surface’s properties, such as height, temperature, or velocity.
How are gradients mathematically represented?
Gradients are represented using partial derivatives, which measure the rate of change of a surface’s properties with respect to its coordinates.
What are some practical applications of gradient visualization?
Gradient visualization is used in fields such as fluid dynamics to analyze flow patterns, heat transfer to optimize heat dissipation, and image processing to enhance image quality.