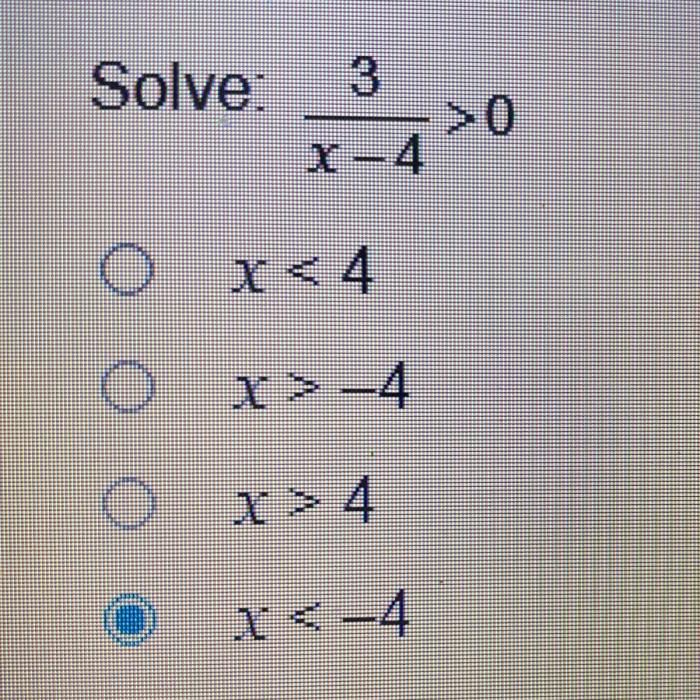Write a compound inequality for the graph shown below. – Embark on an exploration of compound inequalities, a powerful mathematical tool for representing complex relationships graphically. In this comprehensive guide, we delve into the intricacies of compound inequalities, unraveling their types, graphical interpretations, and algebraic solutions. Prepare to unlock the secrets of these mathematical marvels and master the art of expressing complex graphs through the language of inequalities.

Compound inequalities, the focus of our discussion, are mathematical expressions that combine multiple inequalities using logical operators like “and” or “or.” They provide a precise way to describe regions on a graph, enabling us to model and analyze real-world scenarios effectively.

Compound Inequalities: Write A Compound Inequality For The Graph Shown Below.

A compound inequality is a mathematical expression that combines two or more inequalities using the logical operators “and” (∧) or “or” (∨). It represents a region of the coordinate plane that satisfies all or some of the individual inequalities.

Types of Compound Inequalities

• Conjunction (And) Inequality:The region that satisfies both inequalities. It is represented as x∈ A∧ x∈ B, where Aand Bare the individual inequalities.
• Disjunction (Or) Inequality:The region that satisfies at least one of the inequalities. It is represented as x∈ A∨ x∈ B, where Aand Bare the individual inequalities.

Graphical Representation, Write a compound inequality for the graph shown below.

Compound inequalities can be represented graphically by shading the regions that satisfy the inequalities. The shaded region for a conjunction inequality is the intersection of the shaded regions for the individual inequalities, while the shaded region for a disjunction inequality is the union of the shaded regions for the individual inequalities.

Example

Consider the graph of the compound inequality x> 2 ∧ x < 5. The shaded region represents the region where xis greater than 2 and less than 5. This region is the intersection of the shaded regions for the individual inequalities x> 2 and x< 5.

FAQs

What are the different types of compound inequalities?

Compound inequalities can be classified into two main types: conjunctive inequalities (joined by “and”) and disjunctive inequalities (joined by “or”).

How do I graph a compound inequality?

To graph a compound inequality, first graph each individual inequality separately. Then, shade the region that satisfies both (for conjunctive) or either (for disjunctive) of the inequalities.

What are some real-world applications of compound inequalities?

Compound inequalities are used in various fields, such as economics to model constraints on resources, in physics to describe motion with boundaries, and in engineering to design structures within specified limits.